MATERI DAN CONTOH SOAL HIPERBOLA
|
Hiperbolaadalah tempat kedudukan titik-titik yang selisih jaraknya terhadap dua titik tertentu selalu tetap. Dua titik tertentu itu disebut fokus hiperbola.
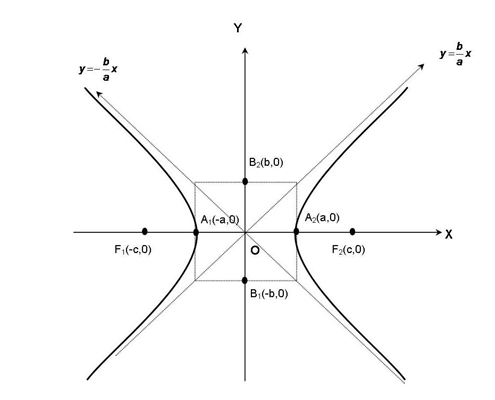
Hiperbola yang berpusat di titik O(0,0).
• F1 (-c, 0)dan F2 ( c, 0)adalah titik fokus hiperbola yang jaraknya 2c. Sementara selisih jarak yang tetap itu adalah 2a.
• Sumbu utama adalah sumbu x, sedangkan sumbu sekawan adalah sumbu y.
• Sumbu mayor adalah A1A2, panjangnya 2a. Sumbu minor adalah B1B2, panjangnya 2b.
• Titik A1 dan A2 disebut titik puncak hiperbola yang merupakan titik potong hiperbola dengan sumbu mayor.
• Lactus rectum adalah garis vertikal yang melalui salah satu fokus, tegak lurus sumbu mayor, dan memotong hiperbola di dua titik. Panjang lactus rektum adalah
2b2
a
• Persamaan asimtot hiperbola adalah
• Eksentrisitas = e = c , dengan e > 1.
a
• Persamaan garis direktriks adalah
• Ketentuan khusus pada hiperbola yaitu c2 = a2 + b2.
Persamaan Hiperbola a. Persamaan hiperbola yang berpusat di titik (0, 0)
Persamaan hiperbola yang berpusat di titik (0, 0) dengan sumbu utamanya sumbu x adalah
x2 − y2 = 1
a2 b2
Titik fokus adalah F1(c, 0) dan F2(-c, 0).
Titik puncak adalah A1(a, 0) dan A2(-a, 0).
Persamaan asimtotnya adalah
Bagaimana jika sumbu utamanya adalah sumbu y
Persamaan hiperbola yang berpusat di titik (0, 0) dengan sumbu utamanya sumbu y adalah
y2 − x2 = 1
a2 b2
Titik fokus adalah F1(0, c) dan F2(0, -c).
Titik puncak adalah A1(0, a) dan A2(0, -a).
Persamaan asimtotnya adalah
Contoh soal :
1. Diketahui persamaan hiperbola 4x2 – 9y2 = 36.
Tentukanlah :
a.Koordinat pusat
b.Koordinat titik puncak
c.Koordinat titik focus
d.Persamaan garis direktriks
e. Persamaan garis asimtot
f. Panjang latus rectum
g. eksentrisitas
d. Persamaan garis direktriks
h. sketsa grafiknya
Penyelesaian:
4x2 – 9y2=36 ↔ x2 − y2=1
9 4
a2=9↔a=3 b2=4↔b=2
a. koordinat titik pusatnya adalah ( 0,0)!
b. koordinat titik puncaknya (a,0) dan (-a,0) adalah (3,0) dan (-3,0)
c. c=√a2+b2= √9+4=√13
koordinat titik fokusnya F1 (-c,0) dan F2 (c,0) adalah F1 ( √13, 0) dan F2 ( √13,0)
d. Persamaan garis direktriksnya adalah
x = a2 = 9 = 9 √13 dan x = −a2 = −9 √13
c √13 13 c 13
e. Persamaan garis asimtotnya adalah
y = b x = 2 x dan y = − bx = −2 x
a 3 a 3
e. Panjang latus rectum :
L = 2b2 = 2.4 = 8
a 3 3
f. Nilai eksentrisitas
e = c = √13
a 3
Tag :
Matematika


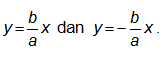
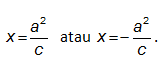
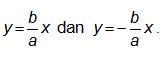
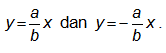

0 Komentar untuk "Materi dan contoh soal Irisan Kerucut HIPERBOLA"