Contoh Soal Limit Fungsi ini adalah soal yang dihimpun dari berbagai sumber, yang meliputi soal limit fungsi un, soal limit sbmptn, dan soal limit uas sma yang kesemuanya telah dilengkapi dengan pembahasan lengkap. Bagi adik-adik yang ingin mempelajari soal ini, silahkan download pembahasan & soal limit fungsi matematika ini melalui link download yang telah disediakan di bawah. Semoga membantu dan bermanfaat. DISINI
FUNGSI TURUNAN DAN PEMBAHASAN
FUNGSI TURUNAN DAN PEMBAHASAN
- Diketahui f(x) =
. Nilai f‘(4) = …
A. 1/3B. 3/7C. 3/5D. 1E. 4Pembahasan:f(x) =f'(x) =misal : u(x) = 2x + 4u'(x) = 2
v(x) = 1 +v'(x) = 1/2 x-1/2
f'(x) =f'(4) ======
- Luas sebuah kotak tanpa tutup yang alasnya persegi adalah 432 cm2. Agar volume kotak tersebut mencapai maksimum, maka panjang rusuk persegi adalah … cm.A. 6B. 8C. 10D. 12E. 16Pembahasan:misal kita anggap tinggi kotak adalah t dan panjang sisi alas adalah s.Luas kotak tanpa tutup = Luas alas (persegi) + (4 x luas sisi)432 = s2 + (4.s.t)432 = s2 + 4tsKarena yang diminta dalam soal adalah panjang sisi persegi, maka kita buat persamaan dalam variable s.432 – s2 = 4ts108/s – s/4 = tVolume = v(x) = s2t= s2(108/s – s/4)= 108s – s3/4Agar volume kotak maksimum maka :v'(x) = 0108 – 3s2/4 = 0108 = 3s2/4144 = s212 = s
- Grafik fungsi f(x) = x3 + ax2 + bx + c hanya turun pada interval –1 < x < 5. Nilai a + b = …A. – 21B. – 9C. 9D. 21E. 24Pembahasan:f'(x) < 03x2 + 2ax + b < 0Karena turun pada interval –1 < x < 5, itu artinya HP dari f'(x) adalah x1 = -1 atau x2 = 5. Jadif'(x) = (x + 1)(x – 5)= x2 – 4x – 53x2 + 2ax + b = 3(x2 – 4x – 5)3x2 + 2ax + b = 3x2 – 12x – 152a = -12
a = -6
b = -15a + b = -6 + (-15) = -21
4. Untuk Mendapatkan Soal Selanjutnya Silahkan Klik Link Download di Bawah ini !
FUNGSI KOMPOSISI DAN PEMBAHASAN
Soal No. 1
Diberikan fungsi-fungsi sebagai berikut:
f(x) = 2 + x
g(x) = x2 − 1
h(x) = 2x
Tentukan rumus dari (h o g o f)(x)
Pembahasan:
Bisa dengan cara satu-satu dulu, mulai dari g bundaran f
(g o f)(x) = (2 + x)2 − 1
= x2 + 4x + 4 − 1
= x2 + 4x + 3
Masukkan hasilnya ke fungsi h(x) sehingga didapatkan
(h o g o f)(x) = 2(x2 + 4x + 3)
= 2x2 + 8x + 6
Diberikan fungsi-fungsi sebagai berikut:
f(x) = 2 + x
g(x) = x2 − 1
h(x) = 2x
Tentukan rumus dari (h o g o f)(x)
Pembahasan:
Bisa dengan cara satu-satu dulu, mulai dari g bundaran f
(g o f)(x) = (2 + x)2 − 1
= x2 + 4x + 4 − 1
= x2 + 4x + 3
Masukkan hasilnya ke fungsi h(x) sehingga didapatkan
(h o g o f)(x) = 2(x2 + 4x + 3)
= 2x2 + 8x + 6
MATRIKS DAN PEMBAHASAN
Soal No. 1
Matriks P dan matriks Q sebagai berikut

Tentukan matriks PQ
Pembahasan
Perkalian dua buah matriks

Soal No. 2
Tentukan nilai a + b + x + y dari matriks-matriks berikut ini

Diketahui bahwa P = Q
Pembahasan
Kesamaan dua buah matriks, terlihat bahwa

3a = 9 → a = 3
2b = 10 → b = 5
2x = 12 → x = 6
y = 6
y = 2
Sehingga:
a + b + x + y = 3 + 5 + 6 + 2 = 16
Soal No. 3
Tentukan determinan dari matriks A berikut ini

Pembahasan
Menentukan determinan matriks ordo 2 x 2
det A = |A| = ad − bc = (5)(2) − (1)(−3) = 10 + 3 = 13
Soal No. 4
Diberikan sebuah matriks

Tentukan invers dari matriks P
Pembahasan
Invers matriks 2 x 2

Soal No. 5
Tentukan tranpose dari matriks A berikut ini

Pembahasan
Transpose sebuah matriks diperoleh dengan mengubah posisi baris menjadi kolom seperti contoh berikut:

Matriks P dan matriks Q sebagai berikut
Tentukan matriks PQ
Pembahasan
Perkalian dua buah matriks
Soal No. 2
Tentukan nilai a + b + x + y dari matriks-matriks berikut ini
Diketahui bahwa P = Q
Pembahasan
Kesamaan dua buah matriks, terlihat bahwa
3a = 9 → a = 3
2b = 10 → b = 5
2x = 12 → x = 6
y = 6
y = 2
Sehingga:
a + b + x + y = 3 + 5 + 6 + 2 = 16
Soal No. 3
Tentukan determinan dari matriks A berikut ini
Pembahasan
Menentukan determinan matriks ordo 2 x 2
det A = |A| = ad − bc = (5)(2) − (1)(−3) = 10 + 3 = 13
Soal No. 4
Diberikan sebuah matriks
Tentukan invers dari matriks P
Pembahasan
Invers matriks 2 x 2
Soal No. 5
Tentukan tranpose dari matriks A berikut ini
Pembahasan
Transpose sebuah matriks diperoleh dengan mengubah posisi baris menjadi kolom seperti contoh berikut:
INTEGRAL DAN PEMBAHASAN
Soal No. 1
Tentukan:
∫ (3x + 7)5 dx
Pembahasan
Bawa ke bentuk ∫ vn dv
Misal:
v = (3x + 5) dengan demikian:
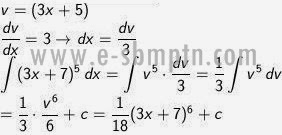
Soal No. 2
Tentukan dengan menggunakan metode substitusi aljabar :
∫ (2x + 10)3 dx
Pembahasan
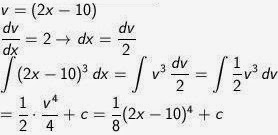
Soal No. 3
Tentukan hasil dari:
∫ √(3x + 6) dx
Pembahasan
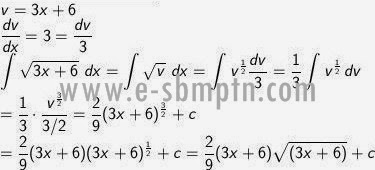
Soal No. 4
Tentukan hasil dari:
∫ 3√(3x + 6) dx
Pembahasan
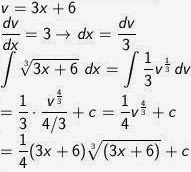
Soal No. 5
Tentukan hasil dari:
∫ (3x3 + 5)7 x2 dx
Pembahasan
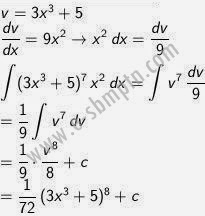
Soal No.6
Tentukan hasil dari:
∫ 3√(12 x5 − 7) x4 dx
Pembahasan
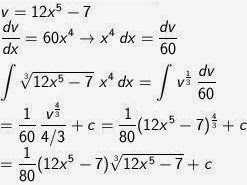
Soal No. 7
Hasil dari

adalah....

Pembahasan

Tentukan:
∫ (3x + 7)5 dx
Pembahasan
Bawa ke bentuk ∫ vn dv
Misal:
v = (3x + 5) dengan demikian:
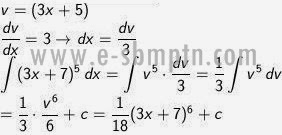
Soal No. 2
Tentukan dengan menggunakan metode substitusi aljabar :
∫ (2x + 10)3 dx
Pembahasan
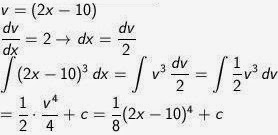
Soal No. 3
Tentukan hasil dari:
∫ √(3x + 6) dx
Pembahasan
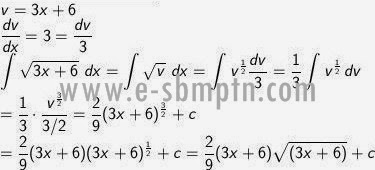
Soal No. 4
Tentukan hasil dari:
∫ 3√(3x + 6) dx
Pembahasan
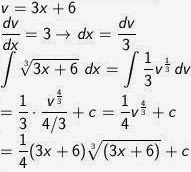
Soal No. 5
Tentukan hasil dari:
∫ (3x3 + 5)7 x2 dx
Pembahasan
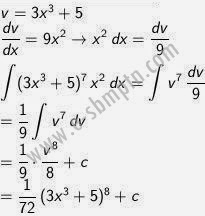
Soal No.6
Tentukan hasil dari:
∫ 3√(12 x5 − 7) x4 dx
Pembahasan
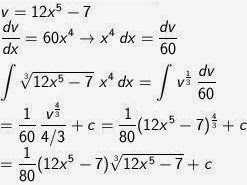
Soal No. 7
Hasil dari

adalah....

Pembahasan

FUNGSI TURUNAN DAN PEMBAHASAN
1. Fungsi f ditentukan oleh  dan f ‘ adalah turunan pertama dari f. Maka nilai dari f ‘(1) = ….
dan f ‘ adalah turunan pertama dari f. Maka nilai dari f ‘(1) = ….
a.
b.
c.
d.
e.
Pembahasan:



2. Turunan pertama fungsi adalah f ‘(x) = ….
adalah f ‘(x) = ….
a.
b.
c.
d.
e.
Pembahasan:



3. Diketahui dan f ‘(x) adalah turunan pertama dari f(x). Maka nilai dari f ‘(-1) = ….
dan f ‘(x) adalah turunan pertama dari f(x). Maka nilai dari f ‘(-1) = ….
a. 4
b. 12
c. 16
d. 84
e. 112
Pembahasan:

misalkan u = 3x + 4 maka u’ = 3 dan n = 4
gunakan aturan rantai, maka :

4. Turunan pertama fungsi adalah f ‘(x) = ….
adalah f ‘(x) = ….
a.
b.
c.
d.
e.
Pembahasan:
 , nyatakan dalam bentuk pangkat
, nyatakan dalam bentuk pangkat


5. Turunan pertama dari adalah f ‘(x) = …
adalah f ‘(x) = …
a.
b.
c.
d.
e.
Pembahasan:
 nyatakan dalam bentuk pangkat
nyatakan dalam bentuk pangkat

maka :

a.
b.
c.
d.
e.
Pembahasan:
2. Turunan pertama fungsi
a.
b.
c.
d.
e.
Pembahasan:
3. Diketahui
a. 4
b. 12
c. 16
d. 84
e. 112
Pembahasan:
misalkan u = 3x + 4 maka u’ = 3 dan n = 4
gunakan aturan rantai, maka :
4. Turunan pertama fungsi
a.
b.
c.
d.
e.
Pembahasan:
5. Turunan pertama dari
a.
b.
c.
d.
e.
Pembahasan:
maka :


0 Komentar untuk "Kumpulan Soal UN Matematika dan Kunci Jawaban Kelas XII SMA TA 2014/2015"